Maurice S. Fabien
Basic information
Primary research interests are the application, theory, and discretization of partial differential equations and high performance computing; discontinuous Galerkin methods, spectral/geometric/algebraic multigrid solvers, and accelerators (GPU, KNL, etc.).
Since 2007, I have been very involved with the recruitment, retention, and outreach for women, underrepresented minorities, and socioeconomically underprivileged in science, technology, engineering, and mathematics in higher education.
Since 2007, I have been very involved with the recruitment, retention, and outreach for women, underrepresented minorities, and socioeconomically underprivileged in science, technology, engineering, and mathematics in higher education.
Research
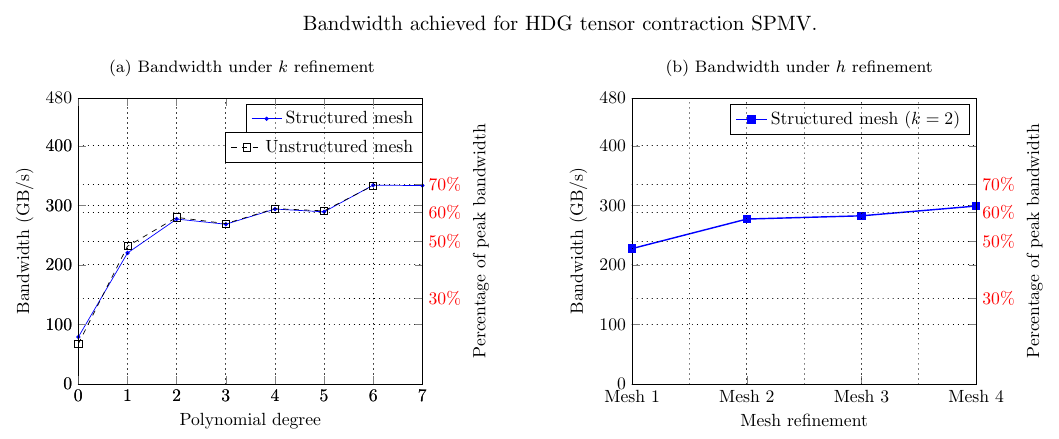
High Performance Computing, Parallel Computing, and Performance Analysis
Modern many-core architectures possess FLOPs in abundance. However, they also have sophisticated user-managed memory hierarchies. Furthermore, the floating point performance is rapidly outpacing memory operation performance. A large class of problems are bandwidth bound, and for these type of problems the best performance improvements come from proper bandwidth utilization.
Flow and Transport in Porous Media
My research has demonstrated that the use of high order discontinuous finite element methods can work well for flow and transport in porous media. On coarser meshes, we can obtain great accuracy by enriching the approximation space:

 Our methods have been thoroughly tested in multiple dimensions for single-phase, two-phase, and three-phase flows. We employ compatible hybridizable discretizations to ensure high accuracy, computational efficiency, and mass-conserving numerical approximations of multiphase flows and transport.
Our methods have been thoroughly tested in multiple dimensions for single-phase, two-phase, and three-phase flows. We employ compatible hybridizable discretizations to ensure high accuracy, computational efficiency, and mass-conserving numerical approximations of multiphase flows and transport.



 A growing interest in phase-field modeling of multiphase flows has occured. They are a popular model for solving interfacial problems. Below are some simulations from the Navier-Stokes-Allen-Cahn model ('kissing droplets' and 'mean curvature flow snap-off').
A growing interest in phase-field modeling of multiphase flows has occured. They are a popular model for solving interfacial problems. Below are some simulations from the Navier-Stokes-Allen-Cahn model ('kissing droplets' and 'mean curvature flow snap-off').










Discontinuous Galerkin Methods
Discontinuous Galerkin (DG) methods are a powerful class of finite element techniques for approximating solutions to partial differential equations. My interest in DG stems from its strong mathematical theory and robust approximation capabilities for PDEs.
Classical DG methods give rise to an abundance of degrees of freedom, which poses major challenges for implicit PDEs. The Hybridizable discontinuous Galerkin (HDG) method remedies this by introducing additional Lagrange multiplier unknowns on the element boundaries. With a judicious choice of numerical flux and trace, the HDG method is capable of statically condensing its interior unknowns. This results in a smaller globally coupled linear system in terms of the additional hybrid unknowns only.
A depiction of the Hybridizable discontinuous Galerkin method is given below.




Spectral/Algebraic/Geometric Multigrid
Multigrid methods are very effective multilevel solvers for linear systems. Multigrid methods takes advantage of a hierarchy of grids or discretizations and reduces the error over a range of frequencies simultaneously. My work has examined parallel implementations of h-multigrid, p-multigrid, and algebraic multigrid, applied to linear systems arising from DG discretizations; as well as exporing efficient relaxation, prolongation, and restrication operators.

Spectral Methods
Spectral methods are a class of discretization techniques for partial differential equations that are capable of producing highly accurate approximations. If the underlying function one is approximating is smooth, spectral methods have the fastest possible convergence. See my Master's thesis for an exploration of these methods within the context of hyperbolic PDEs.
Maurice S. Fabien 2020-